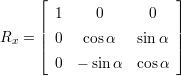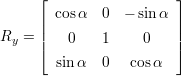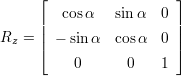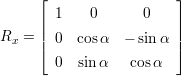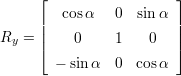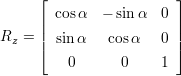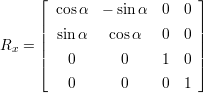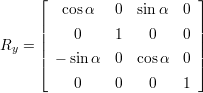Teil I
Mathematik und zugehöriges
Autor: Thomas Block
Dies ist eine Sammlung von mathematischen Beschreibungen und Anleitungen zu den Gebieten Mathematische Grundlagen, Computergrafik.
Inhaltsverzeichnis
1 Mathematische Grundlagen
1.1 Determinanten
1.2 Lineare Gleichungssysteme
1.3 Matrizen und Determinanten
1.3.1 Eingenwerte und -vektoren
1.4 Die Laplace Transformation
1.4.1 Rechenregeln der Laplace Transformation
1.5 Die Laplace Ummkehrtransformation
1.5.0.1 Partialbruchzerlegung
1.5.0.2 Entwicklung in eine Laurentreihe
1.5.0.3 Residuenkalkül
1.6 Fouriertransformation
1.6.1 Umrechnungsformeln
1.6.1.1 Rechenregeln
1.6.1.2 Rechenhilfen
1.6.1.3 Rücktransformation
1.7 Die Z-Transformation
1.7.1 Umkehrtransformation
1.7.2 Rechenregeln
2 Mathematische Grundlagen für die Computergrafik
2.1 Transformationen
2.1.1 Geometrische Transformation
2.1.2 Koordinatentransformation
2.2 Homogene Koordinaten
2.2.1 Überführung einer Vektorgleichung in homogene Matrizenschreibweise
2.3 Die verschiedenen Projektionsarten
2.3.1 Die perspektivische Projektion
2.3.2 Die Parallelprojektion
Kapitel 1
Mathematische Grundlagen
1.1 Determinanten
Autor: Thomas Block
Sind an1,an2 ann n Vektoren der Dimension n, so ordnet die Determinante
ann n Vektoren der Dimension n, so ordnet die Determinante
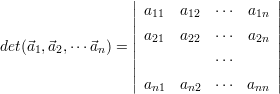 | (1.1) |
den Vektoren genau eine reelle Zahl d zu.
Berechnung der Determinante:
Streicht man die i-te Zeile und k-te Spalte der Determinate D, so wird die Determinate der Ordnung (n-1) aus den
restlichen Elementen als Unterdeterminante Dik bezeichnet. Der Ausdruck Aik = (-1)i+kDik heißt dann adjungierte
Unterdeterminante.
Damit lässt sich die Determinate D berechnen zu:
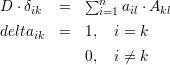 | (1.2) |
1.2 Lineare Gleichungssysteme
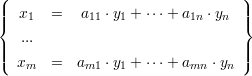
implizierte Summierung |
||
xi | = | aij ⋅ yj |
mit i | = | 1  m, j = 1 m, j = 1 n n |
 | (1.3) |
1.3 Matrizen und Determinanten
Mit
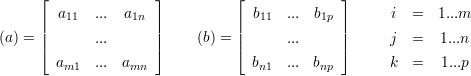 | (1.4) |
gilt:
| Konst. Faktor: | (c) = m ⋅ (a), | cij = m ⋅ aij |
| Addition: | (c) = (a) + (b), | cij = aij + bij |
| Multiplikation: | (c) = (a) ⋅ (b), | cik = aij ⋅ bjk |
| Transponierte: | (aij)T = aji | |
((a) ⋅ (b) (x))T (x))T | = (x)T  (b)T ⋅ (a)T (b)T ⋅ (a)T |
|
| Inverse (m=n): | (a) ⋅ (a)-1 | = Einheitsmatrix (e) |
| (a)-1 = (c)T ∕det(a) | mit cij = (-1)i+j ⋅ detij(a) | |
Hierbei ist detij die Determinante mit ausgestrichener Zeile i und Spalte j
| ||
1.3.1 Eingenwerte und -vektoren
| Die Eigenwerte Λi einer Matrix erhält man durch Lösen von | det((a) - λ ⋅ (e)) = 0. |
Die Eigenvektoren 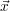 i erhält man durch Lösen von i erhält man durch Lösen von | ((a) - λi ⋅ (e)) ⋅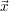 i = i = 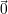 . . |
1.4 Die Laplace Transformation
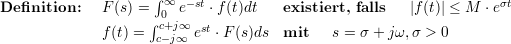 | (1.5) |
1.4.1 Rechenregeln der Laplace Transformation
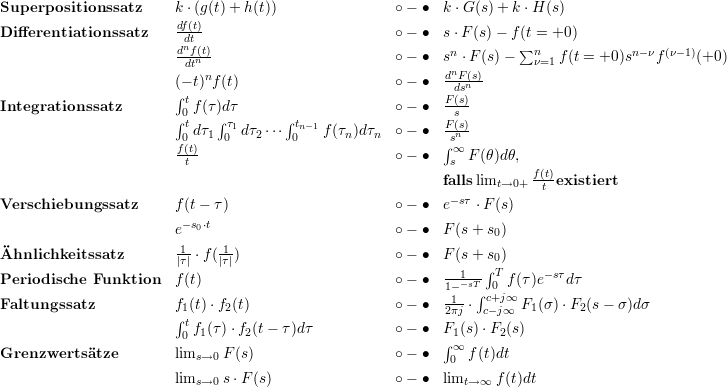
| Hilfen: | f(t) ⋅ sin(at) | ∘-∙ | 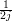 ⋅ (F(s - ja) - F(s + ja)) ⋅ (F(s - ja) - F(s + ja)) |
| f(t) ⋅ cos(at) | ∘-∙ | 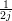 ⋅ (F(s - ja) + F(s + ja)) ⋅ (F(s - ja) + F(s + ja)) |
|
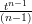 ⋅ e±at ⋅ e±at | ∘-∙ | (p ± a)-n | |
1.5 Die Laplace Ummkehrtransformation
Wege zur Berechnung des Umkehrintegrals ∫ c-j∞c+j∞est ⋅ F(s)ds.
1.5.0.1 Partialbruchzerlegung
Es sei m die Anzahl der Polstellen von F(s) mit maximalem Grad n.
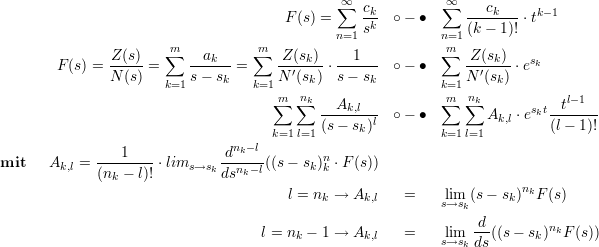
1.5.0.2 Entwicklung in eine Laurentreihe
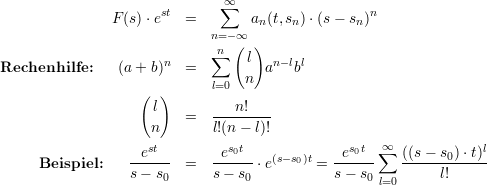
1.5.0.3 Residuenkalkül
Vorraussetzungen: Es sei lims→∞|F(s)| = 0, f(t) = 0 für m < 0, dann gilt:
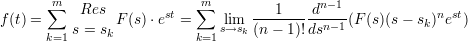
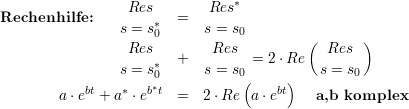
1.6 Fouriertransformation
1.6.1 Umrechnungsformeln
In der linken Spalte ist die Zielfuntion angegeben in der zugehörigen Zeile die jeweiligen Ausgangsfunktionen und deren Berechnungsvorschrift zur Erreichung der Zielfunktion.
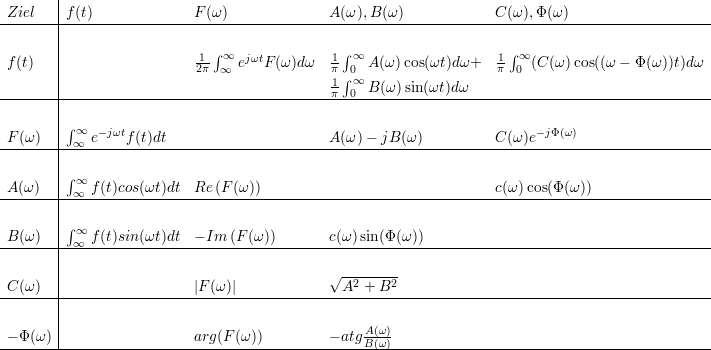 | (1.6) |
1.6.1.1 Rechenregeln
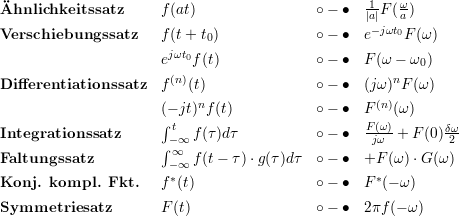 | (1.7) |
1.6.1.2 Rechenhilfen
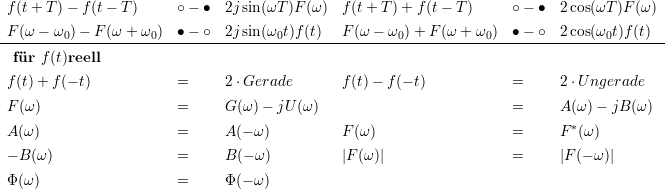 | (1.8) |
1.6.1.3 Rücktransformation
Vorraussetungen:
- F(ω) stetig auf ℜ und absolut integrierbar
- H+ = positive komplexe Halbebene, H- = negative komplexe Halbebene
- setze ω = z
- limz→∞F(z) = 0
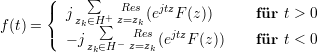 | (1.9) |
1.7 Die Z-Transformation
Definition:
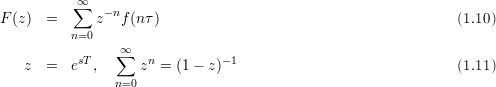
1.7.1 Umkehrtransformation
Vorraussetzungen: F(z) ist holomorph in einem Gebiet |z| > R und limz→∞F(z) < ∞
mit Residuum:
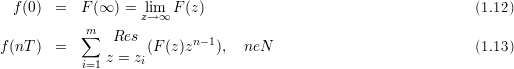
mit Laurent Reihe: Der Integrant f(z) ⋅ zn-1 wird in eine Laurent Reihe entwickelt. Die Zeitfunktion ist dann der Koeffizient -1 der Lauren Reihe, also f(nτ) = A-1.
Bei der Entwicklung in eine Reihe sind folgende Beziehungen nützlich:
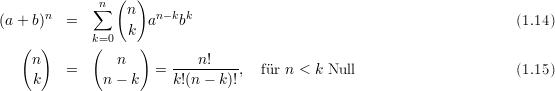
Beispiele:
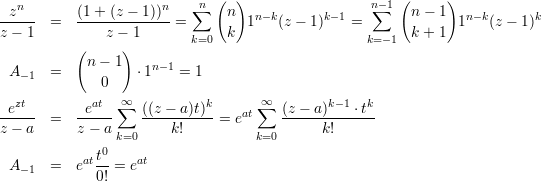
Bei wesentlicher Singularität:

1.7.2 Rechenregeln
Es sei fn = f(nτ), dann gilt:
 | (1.17) |
Chapter 2
Mathematische Grundlagen für die Computergrafik
Autor: Thomas Block
In diesem Kapitel werden die mathematischen Grundlagen dargestellt, die notwendig sind, um dreidimensionale Objekte mit Hilfe eines Computers grafisch darzustellen und zu animieren. Die mathematischen Grundlagen sind in /86 Ba./ und /87 Pl./ zu finden.
2.1 Transformationen
Man unterscheidet in der Mathematik zwischen geometrischer Transformation und Koordinatentransformation. Beide Transformationen lassen sich dabei durch Bilden der Inversen ineinander überführen.
Als Schreibweise von Vektoren und Matrizen wurde in diesem Kapitel die in der Computergrafik übliche übernommen. D.h.
Vektoren sind ohne sonstige Anmerkung als Zeilenvektoren 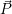 = (x,y,z) definiert. Matrizen werden deshalb rechts
anmultipliziert. Möchte man die übliche mathematische Schreibweise benutzten, so sind alle Vektoren und Matrizen zu
transponieren. Sind z.B. M1,M2
= (x,y,z) definiert. Matrizen werden deshalb rechts
anmultipliziert. Möchte man die übliche mathematische Schreibweise benutzten, so sind alle Vektoren und Matrizen zu
transponieren. Sind z.B. M1,M2 Mi Matrizen, so gilt : (M1 ⋅ M2
Mi Matrizen, so gilt : (M1 ⋅ M2 Mi)T = MiT
Mi)T = MiT  M2T ⋅ M1T
M2T ⋅ M1T
2.1.1 Geometrische Transformation
Bei der geometrische Transformation überführt man eine Menge von Punkten mit den Koordinaten (xi,yi) durch eine mathematische Operation in eine Menge von Punkten mit den neuen Koordinaten (xi′,yi′). Durch eine solche Transformation kann man also ein Objekt O in ein Objekt O’ überführen (Abbildung 2.1.1). Eine solche Operation stellt z.B. eine Multiplikation eines Vektor mit einer Matrix dar. Der Vektor enthält dabei die Punktkoordinaten und die Matrix die gewünschte Transformationsart.
Geometrische Transformation Für die Computergrafik wichtige Transformationen sind dabei die Translation, Rotation und Skalierung. Die zugehörigen Matrizen sehen dazu wie folgt aus :
- Translation:
- Werden Koordinaten nicht als homogen eingeführt (siehe Abschnitt 6.2), so ist die Translation eine
Addition einer eindimensionalen Matrix (Vektor)
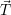 zum Punktvektor
zum Punktvektor 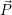 . Die Operation lautet also
:
. Die Operation lautet also
:
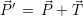
(2.1) - Rotation:
- Die Rotation eines Punktes
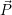 um den Ursprung, erhält man mathematisch durch Multiplikation des Punktes
mit einer Matrix R, also
um den Ursprung, erhält man mathematisch durch Multiplikation des Punktes
mit einer Matrix R, also 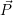 ′ =
′ = 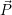 ⋅ R. Da im 3 dimensionalen Raum drei Achsen (x,y,z) existieren, gibt es drei
unterschiedliche Matrizen.
⋅ R. Da im 3 dimensionalen Raum drei Achsen (x,y,z) existieren, gibt es drei
unterschiedliche Matrizen.
- Skalierung:
- Die Skalierung eines Punktes
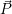 , erhält man durch Multiplikation des Punktes mit der Skaliermatrix S
(
, erhält man durch Multiplikation des Punktes mit der Skaliermatrix S
(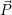 ′ =
′ = 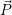 ⋅ S).
⋅ S).
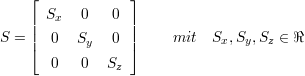 | (2.5) |
Durch Verketten dieser drei Operationen lassen sich sehr komplexe Transformationen aufbauen, in der alle für die Computergrafik relevanten Objektbewegungen ausgeführt werden können.
Eine Verkettung, die oftmals benutzt wird, ist die Rotation um eine beliebige aber bekannte Achse im Raum mit dem
normierten Achsvektor 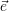 . Diese Rotation kann vereinfacht berechnet werden durch:
. Diese Rotation kann vereinfacht berechnet werden durch:
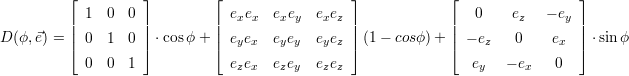 | (2.6) |
2.1.2 Koordinatentransformation
Bei dieser Transformation wird nicht ein Objekt zu einem neuen Ort überführt, sondern ein und dasselbe Objekt in einem neuen Koordinatensystem beschrieben. Eine Menge von Punkten mit den Koordinaten (xi,yi) im Koordinatensystem K wird durch eine mathematische Operation in eine Menge von Punkten mit den neuen Koordinaten (xi′,yi′) im Koordinatensystem K’ (siehe Abbildung 2.1.2) beschrieben.
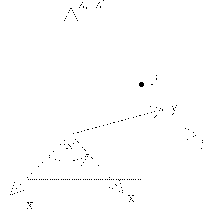
Koordinatentransformation
Gegeben sei der n-dimensionale Vektor 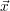 bezüglich der Basix
bezüglich der Basix 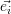 , also
, also 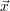 = x1 ⋅
= x1 ⋅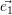 +
+  + xn ⋅
+ xn ⋅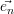 . Gesucht ist die
Transformation T, die
. Gesucht ist die
Transformation T, die 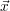 bezüglich der neuen Basis
bezüglich der neuen Basis 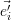 darstellt, also
darstellt, also
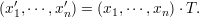 | (2.7) |
Die Inverse Matrix, die gebildet wird aus den Einheitsvekoren der neuen Basis, erfüllt diesen Sachverhalt, man erhält also :
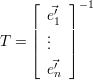 | (2.8) |
Auch hier finden wir als Grundoperationen die Translation, Rotation und Skalierung wieder, die wie folgt aussehen.
- Translation:
- Liegt das Koordinatensystem K’ parallel zum System K und der Ursprung von K’ liegt bei
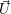 bezogen auf
K, so besitzt der Punkt
bezogen auf
K, so besitzt der Punkt 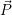 im Koordinatensystem K’ folgende Koordinaten:
im Koordinatensystem K’ folgende Koordinaten:
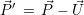
(2.9) - Rotation:
- Liegt das Koordinatensystem K’ verdreht zum Koordinatensystem K und die Ursprünge und Einheiten beider
Koordinatensysteme sind gleich, so läßt sich
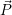 bezogen auf K in K’ beschreiben, indem man den Vektor
bezogen auf K in K’ beschreiben, indem man den Vektor 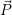 mit einer
Matrix R multipliziert (
mit einer
Matrix R multipliziert (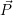 ′ =
′ = 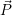 ⋅R). Da im dreidimensionalen Raum drei Drehachsen (x,y,z) existieren, gibt es drei
unterschiedliche Matrizen.
⋅R). Da im dreidimensionalen Raum drei Drehachsen (x,y,z) existieren, gibt es drei
unterschiedliche Matrizen.
- Skalierung:
- Besitzt das Koordinatensystems K’ andere Maßstäbe als K, so erhält man
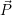 ′ durch Multiplikation von
′ durch Multiplikation von 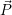 mit
einer Skaliermatrix S (
mit
einer Skaliermatrix S (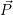 ′ =
′ = 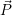 ⋅ S).
⋅ S).
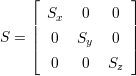 | (2.13) |
, mit Sx,Sy,Sz ∈ℜ
2.2 Homogene Koordinaten
Wie man in den vorhergehenden Abschnitten erkennt, gibt es für die Translation und den übrigen Transformationen keine einheitliche Darstellung. Die Translation wird durch Addition (Subtraktion) eines Vektor gebildet, die übrigen Transformationen durch Multiplikation mit einer Matrix. Um eine einheitliche Darstellung zu erreichen, führt man die homogenen Koordinaten ein. Dabei wird einem 3D Punkt (x,y,z) ein Quadrupel (x*,y*,z*,w) zugeordnet. Die Koordinaten lassen sich mittels

- Translation:
- Liegt das Koordinatensystem K’ parallel zum System K und der Ursprung von K’ liegt bei
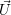 = (Ux,Uy,Uz,1) bezogen auf K, so besitzt der Punkt
= (Ux,Uy,Uz,1) bezogen auf K, so besitzt der Punkt 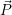 im Koordinatensystem K’ die Koordinaten
im Koordinatensystem K’ die Koordinaten
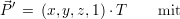
(2.17) 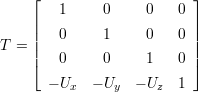
(2.18) - Rotation:
- Liegt das Koordinatensystem K’ verdreht zum Koordinatensystem K und die Ursprünge und Einheiten beider
Koordinatensysteme sind gleich, so läßt sich
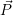 bezogen auf K in K’ beschreiben, indem man
bezogen auf K in K’ beschreiben, indem man 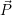 mit einer Matrix M
multipliziert (
mit einer Matrix M
multipliziert (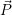 ′ =
′ = 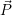 ⋅ R). Da im dreidimensionalen Raum drei Drehachsen (x,y,z) existieren, gibt es drei
unterschiedliche Matrizen.
⋅ R). Da im dreidimensionalen Raum drei Drehachsen (x,y,z) existieren, gibt es drei
unterschiedliche Matrizen.
- Skalierung:
- Besitzt das Koordinatensystems K’ andere Maßstäbe als K, so erhält man
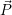 ′ durch Multiplikation von
′ durch Multiplikation von 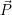 mit
einer Skaliermatrix S (
mit
einer Skaliermatrix S (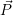 ′ =
′ = 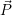 ⋅ S).
⋅ S).
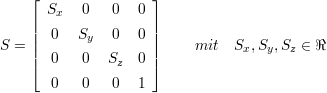
(2.22) - Inverse:
- Die Inverse aus Translation und Rotation und der Multiplikation beider Matrizen läßt sich einfach berechnen. Es
gilt :

2.2.1 Überführung einer Vektorgleichung in homogene Matrizenschreibweise
Liegt eine Gleichung in Vektorform vor, soll aber als Gleichung mit einer homogenen Matrix dargestellt werden, so ist folgende Beziehung sehr hilfreich:
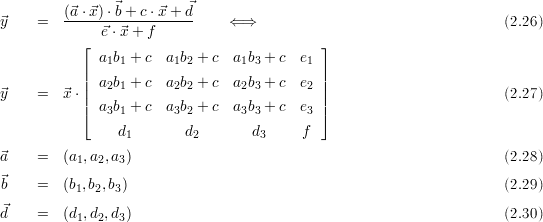
Die Vektoren 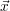 ,
,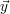 haben dabei die Dimension 3.
haben dabei die Dimension 3.
2.3 Die verschiedenen Projektionsarten
Es existieren zwei verschiedene Projektionsarten, die in noch weitere Spezialfälle unterteilt werden. Zum einen ist dies die parallele Projektion, zum anderen die zentrale oder perspektivische Projektion. Die Projektionsarten sind dabei, wie in Abbildung 2.3 aufgeführt, unterteilt :
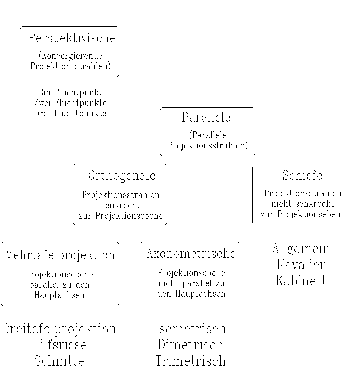
Projektionsarten
2.3.1 Die perspektivische Projektion
Bei der Zentralprojektion wird ein Teilgebiet eines dreidimensionalen Raumes in ein Ebene projeziert. Diese Abbildung bildet die natürlichen Sehvorgänge des menschlichen Auges nach. Der Mittelpunkt der Auglinse befindet sich dabei im Projektionszentrum, die Netzhaut entspricht hierbei der Projektionsebene, die im Abstand z0 vom Augpunkt entfernt liegt.
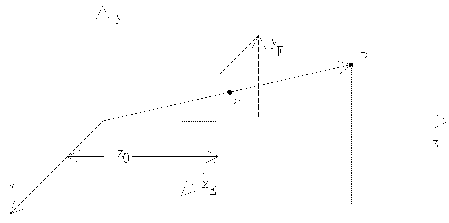
Zentralperspektive 1
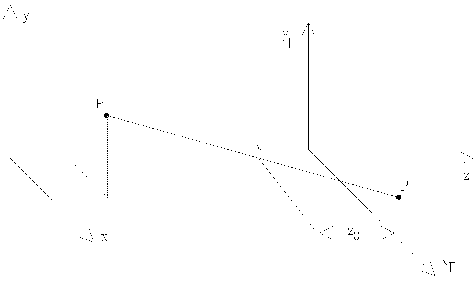
Zentralperspektive 2
Abbildung 2.3.1 zeigt die Projektion eines Punktes P. Das Projektionszentrum liegt dabei im Abstand v vom Ursprung. Die Projektionsebene liegt parallel zu x,y Ebene. Mit Hilfe der Strahlensätze folgt :
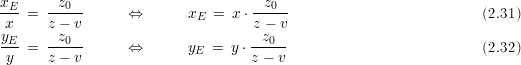
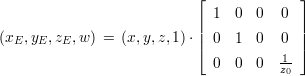 | (2.33) |
Das Gehirn des Menschen korregiert dabei das gespiegelte Bild, so daß es nicht mehr auf dem Kopf steht. Durch die Korrektur erhält man die Projektion nach Abbildung 2.3.1. Legt man den Augpunkt in den Ursprung, so gilt :
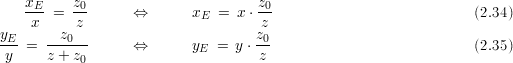
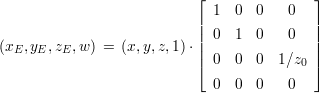 | (2.36) |
Zentralperspektive 3
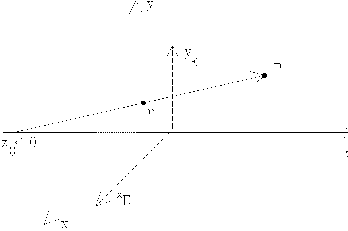
Man kann aber auch die Projektionsebene auf die x-,y-Ebene legen (Abbildung 2.3.1), dann erhält man :
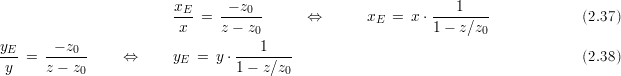
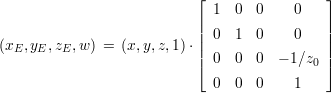 | (2.39) |
Aus der perspektivischen Transformation nach (6.26) lassen sich einige Eigenschaften ablesen :
- Alle Punkte der x, y Ebene bleiben unverändert.
- Alle Parallen zur x-, und y- Achse bleiben nach der Transformation parallel.
- Alle Parallelen zur z-Achse laufen durch den Fluchtpunkt (0,0,z0,1).
- Je weiter ein Objekt vom Projektionszentrum entfernt liegt, desto kleiner erscheint es.
2.3.2 Die Parallelprojektion
Bei der Parallelprojektion werden Objekte parallel zu einer Projektionsrichtung auf die Bildebenen abgebildet. D.h. man
findet die Bildpunkte als Schnittpunkte der Bildebene mit dem Projektionsstrahl, der vom Objektpunkt parallel zur
Projektionsrichtung verläuft. Liegt dabei der Projektionsstrahl senkrecht zur Bildebene, so handelt es sich um die
orthogonale Projektion. Ist die Projektionsrichtung parallel zu einer der drei Hauptachsen, so werden Auf-, Grund- und
Seitenrisse dargestellt. Axonometrische Projektionen sind orthogonale Projektionen, bei denen die Projektionsrichtungen
nicht parallel zu eine der drei Hauptachsen liegt. Nichtorthogonale parallele Projektionen werden schiefe
Parallelprojektion genannt. Die Matrix für die allgemeine Parallelprojektion eines Punktes 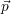 auf eine vorgegebene
Bildebene mit Normalenvektor
auf eine vorgegebene
Bildebene mit Normalenvektor 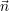 und Ebenenpunkt
und Ebenenpunkt 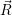 0 in Richtung eines gegebenen Projektionsstrahles
0 in Richtung eines gegebenen Projektionsstrahles 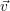 lautet
:
lautet
:
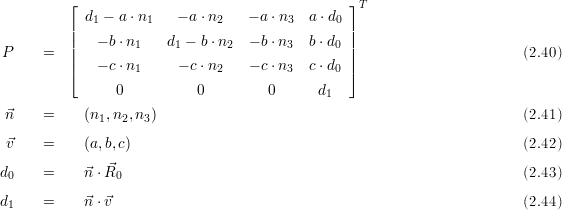
Im folgenden werden einige Projektionsmatrizen für Spezialfälle der Parallelprojektion auf die x-, y- Ebene aufgeführt.
Die orthogonale Projektion auf die x-,y- Ebene erhält man durch weglassen der z- Komponente, also durch die Gleichung
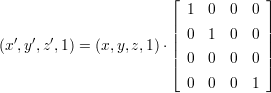 | (2.45) |
.
Die Matrix der Kabinettprojektion (Projektionsrichtung 30 Grad zur x-Achse, Kürzung der z-Komponente um den Faktor 2) lautet :
 | (2.46) |
Die Matrix der Kavalierprojektion (Projektionsrichtung 45 Grad zur x-Achse) lautet :
 | (2.47) |