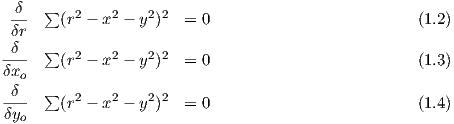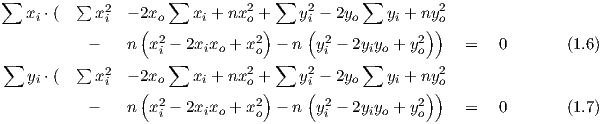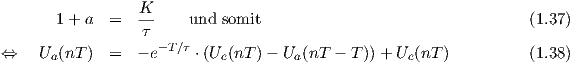Kapitel 1
Meßtechnik

Autor: Thomas Block

Dies ist eine Sammlung von Gebieten zum Thema Meßtechnik im weitesten Sinne (Filter, Regressionsanalyse, Systemidentifikation).

Inhaltsverzeichnis

1 Meßtechnik
 1.1 Regressionsrechnung
  1.1.1 Kreisregression
  1.1.2 Regression für ein System erster Ordnung
  1.1.3 Systemidentifikation
 1.2 Digital-Filter
  1.2.1 Herleitung des Filteralgorithmus’
 1.3 Korrektur von Positionierfehlern

1.1 Regressionsrechnung

Autor: Thomas Block

1.1.1 Kreisregression

Gesucht ist der Kreis, der auf eine Anzahl vom Meßpunkten am besten passt. Ein Kreis mit Mittelpunkt (xo,yo) und Radius r lässt sich beschreiben durch:

y2 = r2 - x2, mit
x=xi-x0,
y = yi-y0
Um die Unbekannten (xo,yo) und r zu ermitteln, wird das Minimum des quadratischen Fehlers der Kreisgleichung zu allen Meßpunkten ermittelt:

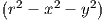∑ ( ) r2 - x2 - y22 = MIN (aus ∑ 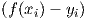(f(xi)- yi)2 = MIN)

Eine notwendige Bedingung für ein Minimum ist, daß die erste partielle Ableitung nach r,xo,yo Null ist, also:

δ ∑ --- (r2 - x2 - y2)2 = 0 (1.2) δr -δ-- ∑ (r2 - x2 - y2)2 = 0 (1.3) δxo -δ- ∑ 2 2 22 δyo (r - x - y ) = 0 (1.4)

Aus Gleichung 1.2 folgt demnach für r≠0:

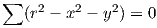∑ (r2 - x2 - y2 ) = 0
(1.5)

Dies in 1.3 und 1.4 eingesetzt und ausmultipliziert, ergibt:

∑ ∑ ∑ ∑ xi ⋅( ∑ x2i - 2xo xi + nx2o + y2i - 2yo yi + ny2o ( ) ( )) - n x2i - 2xixo + x2o - n y2i - 2yiyo + y2o = 0 (1.6) ∑ ∑ 2 ∑ 2 ∑ 2 ∑ 2 yi ⋅( x i - 2(xo xi + nxo +) yi( - 2yo yi + ny)o) - n x2 - 2x x + x2 - n y2- 2yy + y2 = 0 (1.7) i i o o i io o

Nach den Unbekannten geordnet, erhält man folgendes Gleichungssystem:

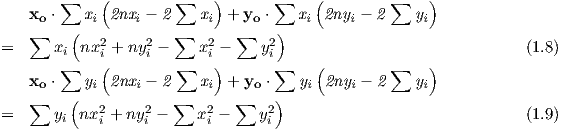
∑ ( ∑ ) ∑ ( ∑ ) xo ⋅ xi 2nxi - 2 xi + yo ⋅ xi 2nyi - 2 yi (1.8)

Hieraus erhält man schließlich für den optimal angepaßten Kreis:

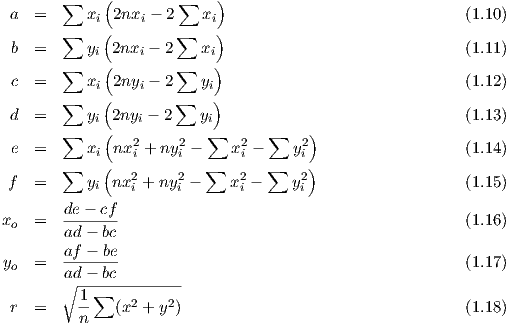
∑ ( ∑ ) a = xi 2nxi - 2 xi (1.9) ∑ ( ∑ ) b = yi(2nxi - 2 xi) (1.10) c = ∑ x 2ny - 2∑ y (1.11) ∑ i( i ∑ i) d = yi 2nyi - 2 yi (1.12) ∑ ( ∑ ∑ ) e = xi nx2i + ny2i - x2i - y2i (1.13) ∑ ( ∑ ∑ ) f = yi nx2i + ny2i - x2i - y2i (1.14) de - cf xo = ------- (1.15) ad - bc yo = af---be (1.16) a∘d---bc--------- 1-∑ 2 2 r = n (x + y ) (1.17)

1.1.2 Regression für ein System erster Ordnung

Gesucht ist die Sprungantwort eines Systems 1. Ordnung, wobei die Zeit in äquidistanten Punkten aufgenommen wird. Die Funktion e-ft kann dann umgeformt werden zu e-ft = e-fnT = fT ⋅ e-n. Es gilt:

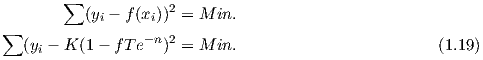
∑ 2 ∑ (yi - f(xi)) = M in. (yi - K (1 - fT e-n)2 = M in. (1.18)
Dies partiell nach den unbekannten K und f abgeleitet und umgeformt, ergibt:
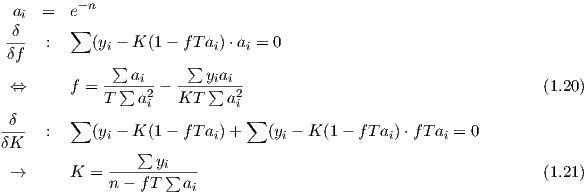
-n ai = e -δ- : ∑ (y - K (1- fT a )⋅a = 0 δf i i i ∑ ai ∑ yiai ⇔ f = T-∑--a2- KT-∑--a2- (1.19) i i δ-- : ∑ (yi - K (1- fT ai)+ ∑ (yi - K (1- fT ai)⋅fT ai = 0 δK ∑ ------yi---- → K = n - fT ∑ ai (1.20)

Für f ergibt sich somit:

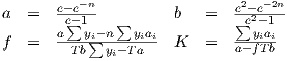a = e-e-n b = e2-e-2n- ae-∑1y-n ∑ ya ∑e2-ya1 f = --Tb∑iyi-Taii K = a-fiTib-
(1.21)

1.1.3 Systemidentifikation

Die diskrete Differenzengleichung des Systems sei:

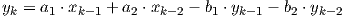yk = a1 ⋅xk- 1 + a2 ⋅xk-2 - b1 ⋅yk-1 - b2 ⋅yk- 2
(1.22)

Gemessen werden die Ausgangswerte yk zu den Eingangswerten xk. Die Werte und die Koeffizienten der DZG werden in jeweils einem Vektor abgebildet:

T x = [x1 x2 ⋅⋅⋅xn ] y = [y1 y2⋅⋅⋅yn]T ab = [a1 a2 - b1 - b2]T (1.23)

Durch Einführung der Hilfsmatrix H läßt sich der Koeffizientenvektor ab mittels der Methode der kleinsten Fehlerquadrate berechnen, man erhält:

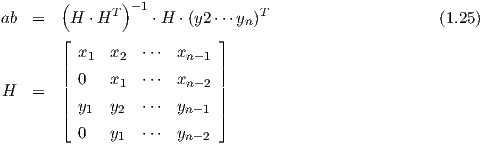
( T )-1 T ab = H ⋅H ⋅H ⋅(y2⋅⋅⋅yn) (1.24) ⌊ ⌋ | x1 x2 ⋅⋅⋅ xn -1 | || 0 x1 ⋅⋅⋅ xn -2 || H = || || ⌈ y1 y2 ⋅⋅⋅ yn -1 ⌉ 0 y1 ⋅⋅⋅ yn -2

Der Verlustvektor ergit sich zu e = [x1⋅⋅⋅xn-1]T - H ⋅ ab und die Verlustfunktion zu V = eT ⋅ e.

Die Z-Übertragungsfunktion des System laute:

yk-= --b1z-1-+-⋅⋅⋅+-bmz--m-- ⋅z-d xk 1 + a1z-1 + ⋅⋅⋅+ amz- m
(1.25)

Gemessen werden die Ausgangswerte yk zu den Eingangswerten xk. Die Daten und die Koeffizienten der DZG werden in jeweils einem Daten- und Parametervektor abgebildet:

ym+d+N = [ym+d ym+d+1 ⋅⋅⋅ym+d+N ]T T dvk = [- yk- 1⋅⋅⋅yk- m | xk-d-1 ⋅⋅⋅xk -d-m] ab = [a1 a2 b1 b2]T (1.26)
Zur Auflösung der Unbekannten werden mindestens N ≥ 2m - 1 Gleichungen benötigt.

Durch Einführung der Hilfsmatrix H läßt sich der Koeffizientenvektor ab mittels der Methode der kleinsten Fehlerquadrate berechnen, man erhält:

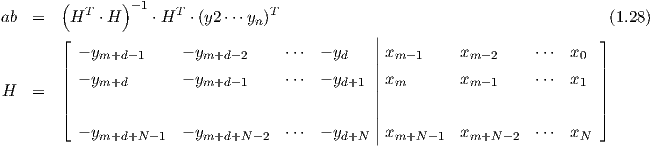
( T ) -1 T T ab = H ⋅H ⋅H ⋅(y2⋅⋅⋅yn) (1.27) ⌊ | ⌋ | - ym+d-1 - ym+d -2 ⋅⋅⋅ - yd |xm -1 xm- 2 ⋅⋅⋅ x0 | || - ym+d - ym+d -1 ⋅⋅⋅ - yd+1 |xm xm- 1 ⋅⋅⋅ x1 || H = || | || ⌈ | ⌉ - ym+d+N -1 - ym+d+N -2 ⋅⋅⋅ - yd+N |xm+N -1 xm+N -2 ⋅⋅⋅ xN

Der Verlustvektor ergit sich zu e = [x1⋅⋅⋅xn-1]T - H ⋅ ab und die Verlustfunktion zu V = eT ⋅ e.

rekursiv

P = HT H ]- 1 (1.28) k k k gk = Pk+1Hk+1 = ----PkHk+1------ (1.29) HTk+1PkHk+1 + 1 abk+1 = abk + gk[yk+1 - HT abk] (1.30) k+1 Pk+1 = [I - gkHTk+1]Pk (1.31)

1.2 Digital-Filter

Autor: Thomas Block

Meßsignale bedürfen zur Signalvorverarbeitung oft der Filterung. Idealerweise sollte dies ein Filter sein, der einerseits keine Phasenverschiebung zum Eingangssignal besitzt, andererseits aber einfach zu implementieren ist und im Online-Betrieb arbeitet. Daraus ergeben sich folgende Möglichkeiten:

  1. Fouriertransformation des Meßsignal, Eliminierung unerwünschter Koeffizienten und Rücktransformation in den Zeitbereich
  2. Speicherung der rohen Meßwerte und anschließende Vorwärts- und Rückwärtsfilterung der Werte, Mitteln der addierten Amplituden
  3. Digitaler Tiefpaß gewünschter Ordnung.

Das folgende Beispiel zeigt die Herleitung und den zugehörigen Programmcode für einen digitalen Tiefpaß erster Ordnung. Dieser besitzt eine Phasenverschiebung, die Abhängig von der Filtergröße ist.

1.2.1 Herleitung des Filteralgorithmus’

Analoge Signale können mittels eines Tiefpasses (TP’s) z.B. durch eine Widerstands-Kondensator-Kombination gefiltert werden. Das Übertragungsverhalten des TP’s kann mit Hilfe der Laplace-Transformation einfach beschrieben werden. Diese Übertragungsfunktion lautet im Laplace-Bereich 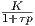-K-- 1+ τp (K ist dabei ein Verstärkungsfaktor und τ die Zeitkonstante des RC-Gliedes).

Für die Nachbildung des Filters auf einen Computer ist es günstig, den Laplace-Übertragungsfaktor in den Z-Bereich zu transformieren, da diese Beschreibungsform eine Umsetzung in die Programmiertechnik ermöglicht. Die Z-Übertragungsfunktion des Tiefpasses lautet:

K∕τ G *(z) = --------1- (1.32) 1+ a⋅z a = - e- T∕τ (1.33)

T ist hierbei die Abtastzeit des digitalen Systems.

Da G*(z) = 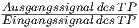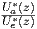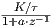AusgangssignaldesTP- EingangssignaldesTP = U*a(z)- U*e(z) = --K∕τ-- 1+a⋅z-1, folgt:

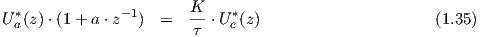
U *a(z)⋅(1+ a ⋅z-1) = K-⋅U *e(z) (1.34) τ
Die Rücktransformation in den Zeitbereich ergibt:
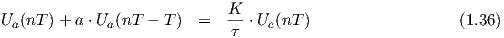
K- Ua(nT )+ a ⋅Ua(nT - T ) = τ ⋅Ue(nT ) (1.35)

Mit der Randbedingung, daß bei einem konstanten Eingangswert der Filterausgang nach definierter Zeit auf den Wert des Eingangssignals kommt (z.B. Ue(nT) = Ua(nT) = 1), folgt:

K 1 + a = -- und somit (1.36) τ -T∕τ ⇔ Ua(nT ) = - e ⋅(Ue (nT )- Ua(nT - T )) + Ue(nT ) (1.37)

Gleichung 1.37 stellt dabei den Implementationsalgorithmus dar. Er besagt: Das Ausgangssignal des TP’s zum Zeitpunkt nT ist die Differenz des Eingangssignals mit dem Ausgangssignal zum Zeitpunkt (n-1)T, bewertet mit der Exponentialfunktion und Addition des Eingangssignales zum Zeitpunkt nT.

Programmiert als Funktion in der Sprache C könnte er folgendermaßen aussehen:

 float Tiefpass (float in, /* Eingangssignal zum Zeitpunkt nT */  
                float out /* Ausgangssignal des TP’s zum Zeitpunkt (n-1)T )  
{  
  extern float a;   /*  = exp (-T/tau) */  
  return a * (in - out) + in;  
}

1.3 Korrektur von Positionierfehlern

Autor: Thomas Block

Werden Maschinenachsen auf eine Sollposition gefahren, so existiert ein Fehler Δ zwischen ausgelesenen Meßwerten und wahrer Position im karesisches Bezugskoordinatensystem K mit den Achsen xK, yK, zK. Dieser Fehler ist dabei abhängig vom Maschinentyp (Änderungen an der Maschine z.B. durch Austausch von Maschinenteilen können dabei Auswirkungen auf die Fehler haben) und von den äußeren Parametern Temperatur ϑ und Alter. Um diese Fehler zu korrigieren, muß die Maschine eingemessen werden.

  1. Im allgemeinsten Fall kann der Fehler abhängig von der Position aller Achsen sein, wobei die Achsen sich gegenseitig beeinflussen, d.h. Δ = f(Achse1,..,Achsen,ϑ).

    Beispiel: Besitzt eine Maschine zwei Achsen y und z mit einer Länge von je 500 mm, die einen Fehler in xK-Richtung produzieren, so gilt ΔxK = f(y,z,ϑ). Für eine Korrektur müsste die y,z-Ebene in Abhängigkeit von der Temperatur gemessen werden. Wird jeder mm ein Meßpunkt aufgenommen so ergeben sich 500*500 Meßpunkte pro Temperaturschritt. Die Anzahl der Punkte potenzieren sich also mit jedem Argument.

  2. Beeinflussen sich die Achsen nicht gegenseitig oder kann die Kopplung vernachlässigt werden, so kann der Fehler jeder Achse für sich gemessen werden, also Δ = f1(Achse1,ϑ) + .. + fn(Achsen,ϑ).

    Im obigen Beispiel müsste nicht eine Ebene abgefahren werden, sondern zwei Geraden (in y- und z-Richtung), also ΔxK = f(y,ϑ) + f(z,ϑ). Wird jeder mm ein Meßpunkt aufgenommen so ergeben sich 500+500 Meßpunkte pro Temperaturschritt. Die Anzahl der Punkte addieren sich also mit jeder zusätzlichen Achse.

  3. Beeinflussen sich die Achsen gegenseitig ist die Kopplung aber in einem weiten Bereich relativ konstant, gilt: Δ = f1(Achse1,ϑ) + .. + fn(Achsen,ϑ) + f(Achse1,..,Achsen,ϑ).

    Scheinbar sind hierbei mehr Meßpunkte aufzunehmen, als im ersten Beispiel. Geht man jedoch davon aus, daß für fi jeder mm für f 1 aber nur alle 5 cm ein Meßpunkt aufgenommen wird, so ergeben sich für das Beispiel 500+500 + 10*10 Meßpunkte pro Temperaturschritt. Die Anzahl der Punkte ist also geringer als im ersten Beispiel.

up